

Eine der wichtigsten Eigenschaften einer Funktion ist ihre Steigung. Wird die Steigung zwischen zwei verschiedenen Punkten der Funktion gesucht,
kann über eine Betrachtung der Differenzen des Funktionswerts und der Variablen die durchschnittliche Steigung in diesem Intervall ermittelt werden.
In diesem Fall wird der tatsächliche Funktionsverlauf durch eine Gerade zwischen den beiden Punkten angenähert. Mit dem bekannten Steigungsdreieck
erhält man dann die bereits erwähnte durchschnittliche Steigung.
Die Gerade, die den Funktionsverlauf annähert, schneidet die Funktion an mindestens zwei Stellen. Aus diesem Grund wird sie auch Sekante der Funktion genannt; die Steigung der Sekanten dementsprechend Sekantensteigung.
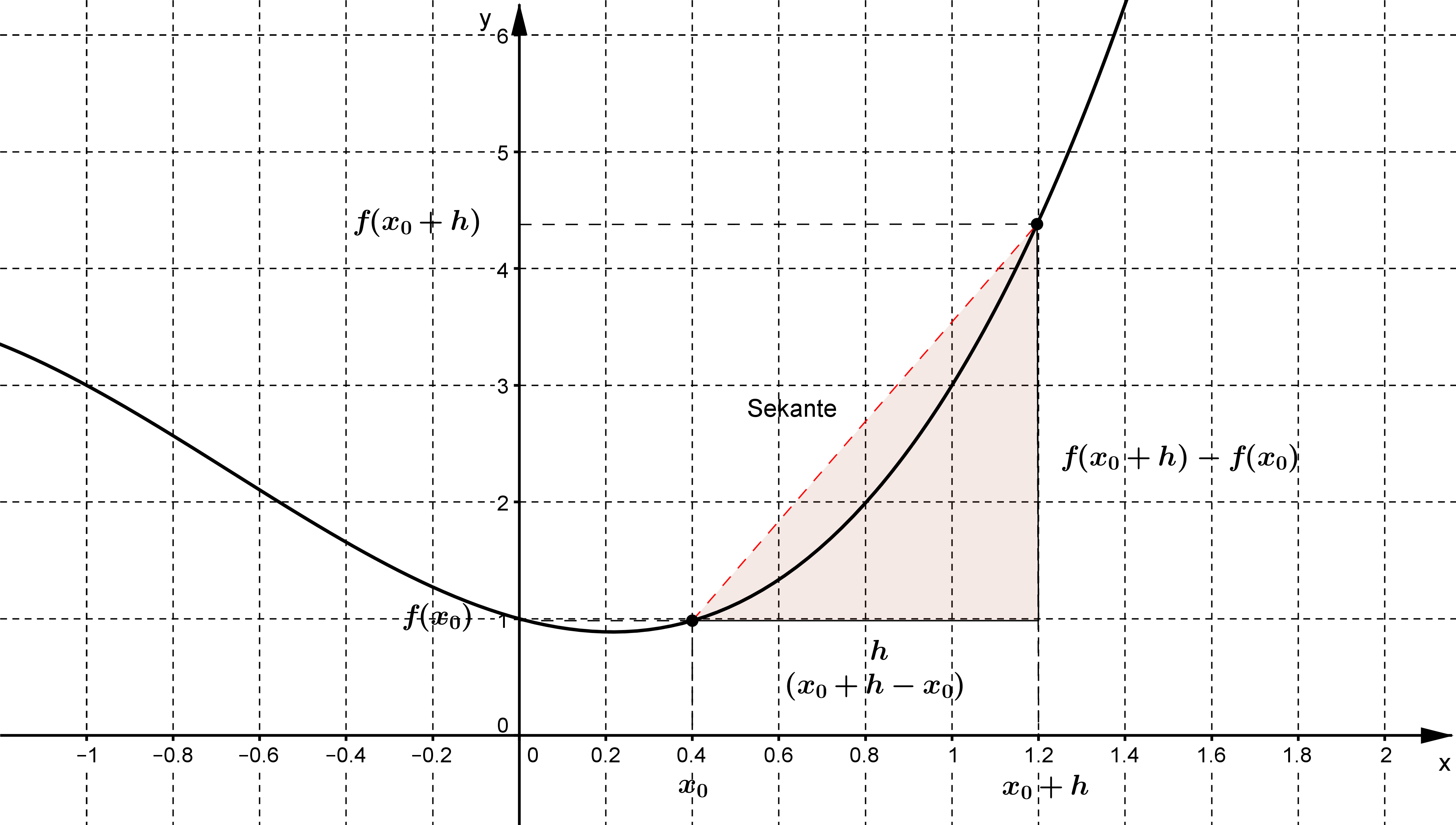
Für die Bestimmung der Steigung der Funktion $f (x)$ in dem Intervall $ I = \{x_0;x_0 + h \}$ kann also geschrieben werden: \begin{align} m = \frac{f(x_0 + h) - f (x_0)}{h} \end{align}
Für die dargestellte Funktion $f(x) = x^3 + 2 x^2 - x+1$ führt das in dem gewählten Intervall $I = \{0,4;1,2\}$ zu folgender Steigung: \begin{align} m &= \frac{f(x_0 + h) - f (x_0)}{h} \\ &= \frac{4,408 - 0,984}{0,8} \\ &= 4,28 \end{align}
Um die Steigung in einem Punkt zu bestimmen, wird nun der Abstand $h$ immer weiter verkleinert, bis der Wert von $h$ von Null nicht mehr zu unterscheiden ist. Man bildet den Grenzwert des Differenzenquotienten für $h \rightarrow 0$.
Die Schreibweise ist dann folgende: \begin{align} m &= \lim_{h \to 0} \frac{f(x_0 + h) - f (x_0)}{h} \end{align} Wenn dieser Grenzwert existiert, dann ist $m$ die Steigung der Tangenten an der Funktion $f$ im Punkt $x_0$ und damit auch die Steigung der Funktion in diesem Punkt. Der Differenzenquotient wird zum Differentialquotienten und so zur Ableitung $f'(x_0)$.
Es gilt also: \begin{align} f'(x_0) &= \lim_{h \to 0} \frac{f(x_0 + h) - f (x_0)}{h} \end{align} Wie man vielleicht erkennt, darf der Grenzübergang $h \rightarrow 0$ nicht ohne weiteres gemacht werden, da in dem Fall durch Null geteilt würde. Die Funktion $f$ muss innerhalb des Differenzenquotienten so umgeformt werden, dass der Nenner im Fall der Grenzübergangs nicht Null wird. Ist das möglich, spricht man davon, dass der Grenzwert existiert.
Für die Beispielfunktion: \begin{align} f'(x) &= \lim_{h \to 0} \frac{f(x_0 + h) - f (x_0)}{h} \\ &= \lim_{h \to 0} \frac{\left(x_0+h\right)^3 + 2 \left(x_0+h \right)^2 - \left(x_0+h\right) +1 - \left(x_0^3+2x_0^2-x_0+1\right)}{h} \\ \\ &= \lim_{h \to 0} \frac{x_0^3 + 3 x_0^2 h + 3 x_0 h^2 + h^3 + 2 \left(x_0^2 + 2 x_0 h + h^2 \right) - x_0 - h + 1 - x_0^3-2x_0^2+x_0-1}{h} \\ \\ &= \lim_{h \to 0} \frac{x_0^3 + 3 x_0^2 h + 3 x_0 h^2 + h^3 + 2 x_0^2 + 4 x_0 h + 2 h^2 - x_0 - h + 1 - x_0^3-2x_0^2+x_0-1}{h} \\ \\ &= \lim_{h \to 0} \frac{x_0^3 - x_0^3 + 2 x_0^2 - 2x_0^2 - x_0 + x_0 + 1 -1 + 3 x_0^2 h + 3 x_0 h^2 + h^3 + 4 x_0 h + 2 h^2 - h }{h} \\ \\ &= \lim_{h \to 0} \frac{3 x_0^2 h + 3 x_0 h^2 + h^3 + 4 x_0 h + 2 h^2 - h }{h} \\ \\ &= \lim_{h \to 0} \frac{3 x_0^2 h}{h} + \frac{3 x_0 h^2}{h} + \frac{h^3}{h} + \frac{4 x_0 h}{h} + \frac{2 h^2}{h} - \frac{h}{h} \\ \\ &= \lim_{h \to 0} 3 x_0^2 + 3 x_0 h + h^2 + 4 x_0 + 2 h - 1 \end{align} In dieser Form darf der Grenzübergang gemacht werden. Mit $h \rightarrow 0$ folgt: \begin{align} f'(x_0) = 3 x_0^2 + 4 x_0 -1 \end{align} Mit dem gewählten Punkt $x_0 = 0,4$ folgt für den Wert der Ableitung $f'(0,4) = 1,08$.
Wird bei der Bestimmung der Steigung der Funktion kein bestimmter Wert für $x_0$ festgelegt, sondern es wird $x_0 = x$ gesetzt, folgt für die Ableitung der Funktionsterm $$ f'(x) = 3 x^2 + 4 x -1 $$ Damit wird die Ableitung an einer Stelle zu einer Ableitungsfunktion für alle $x$.
© mondbrand MMXIX